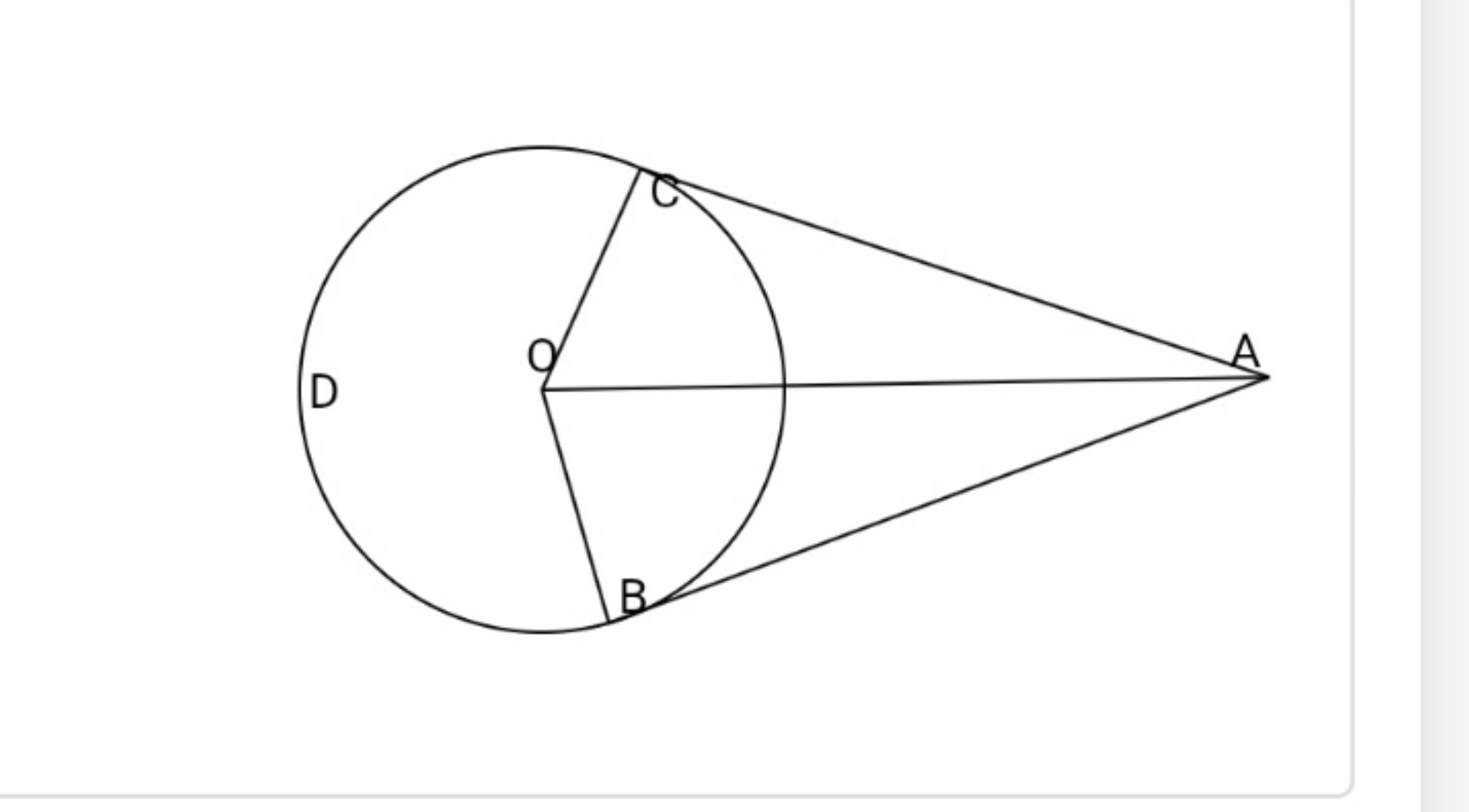
প্রশ্ন: O কেন্দ্রবিশিষ্ট BCD বৃত্তের বহি:স্থ বিন্দু A থেকে 
                বৃত্তে AB ও AC দুটি স্পর্শক। প্রমাণ করো যে, AB = AC.
                
                সমাধান: 
                দেওয়া আছে, O কেন্দ্রবিশিষ্ট BCD বৃত্তে A একটি বহি:স্থ 
                বিন্দু। AB ও AC বৃত্তের যথাক্রমে B ও C বিন্দুতে স্পর্শক। 
                প্রমাণ করতে হবে যে, AB = AC.
                
                অঙ্কন: O,A; O,B এবং O,C যোগ করি।

                প্রমাণ:
                ধাপ ১. যেহেতু AB স্পর্শক এবং OB স্পর্শবিন্দুগামী 
                ব্যাসার্ধ, সেহেতু AB ⊥ OB
                ∴ ∠ABO = 1 সমকোণ।
                অনুরূপভাবে, AC ⊥ OC
                ∴ ∠ACO = 1 সমকোণ।
                সুতরাং, AOB ও AOC উভয়ই সমকোণী ত্রিভুজ।
                
                ধাপ ২.∆AOB এবং ∆AOC সমকোণী ত্রিভুজদ্বয়ে,
                     অতিভুজ OA = অতিভুজ OA [সাধারণ বাহু]
                     OB = OC [একই বৃত্তের ব্যাসার্ধ]
                    ∴ ∆AOB ≅ ∆AOC  [অতিভুজ-বাহু সর্বসমতা ]
                    ∴ AB = AC (প্রমাণিত)